1.2 Tipos de errores: Error absoluto, error relativo, error porcentual, errores de redondeo y truncamiento
Tipos de Errores
Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas. Estos incluyen de truncamiento que resultan de representar aproximadamente un procedimiento matemático exacto, y los errores de redondeo, que resultan de presentar aproximadamente números exactos. Para los tipos de errores, la relación entre el resultado exacto o verdadero y el aproximado está dado por:
E = P* - P
Bien sea una medida directa (la que da el aparato) o indirecta (utilizando una fórmula) existe un tratamiento de los errores de medida. Podemos distinguir dos tipos de errores que se utilizan en los cálculos:
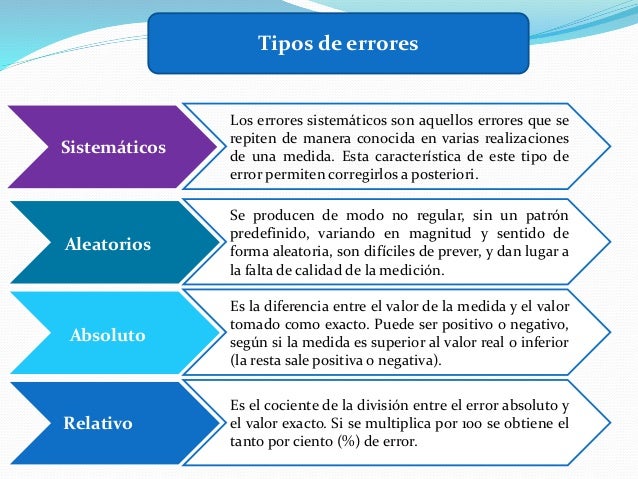
Error absoluto. Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
Sin embargo, para facilitar el manejo y el análisis se emplea el error absoluto definido como:
EA = | P* - P |
Error relativo. Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. no tiene unidades.
Y el error relativo como
ER = | P* - P| / P , si P =/ 0
El error relativo también se puede multiplicar por el 100% para expresarlo como:
ERP = ER x 100
Ejemplo
Supóngase que se tiene que medir la longitud de un puente y de un remache, obteniendose 9 999 y 9 cm, respectivamente. Si los valores son 10 000 y 10 cm, calcúlese a) el error y b) el error relativo porcentual de cada caso.
Solución: a) El error de medicion del puente es:
EA = 10 000 - 9 999 = 1cm
y para el remache es de
EA = 10 - 9 = 1cm
b) El error relativo porcentual para el puente es de:
ERP = 1/ 10 000 x 100% = 0.01%
y para el remache es de
ERP = 1/10 x 100% = 10%
por lo tanto ambas medidas tiene un erro de 1 cm, el error relativo procentual del remache es mucho m´s grande. Se puede concluir que se ha hecho un buen trabajo en la medida del puente, mientras que la estimación para el remache deja mucho que desear.
Errores de Redondeo
Error de redondeo. La casi totalidad de los números reales requieren, para su representación decimal, de una infinidad de dígitos. En la práctica, para su manejo sólo debe considerarse un número finito de dígitos en su representación, procediéndose a su determinación mediante un adecuado redondeo.
Los errores de redondeo se deben a que las computadoras sólo guardan un número finito de cifras significativas durante un cálculo. Las computadoras realizan esta función de maneras diferentes. Por ejemplo, si sólose guardan siete cifras significativas, la computadora puede alamcenar y usar "pi" como "pi" = 3.141592, omitiendo los términos restantes y generando un error de redondeo.
Ya que la mayor parte de las computadoras tiene entre 7 y 14 cifras significativas, los errores de redondeo parecerían no ser muy importantes. Sin embargo, hay dos razones del porqué pueden resultar crítico en algunos métodos numéricos:
Ciertos métodos requieren cantidades extremadamente grandes para obtener una respuesta. En consecuencia, aunque un error de redondeo individual puede ser pequeño, el efecto de acumulación en el transcurso de la gran cantidad de cálculos puede ser significativo.
El efecto del redondeo puede ser exagerado cuando se llevan a cabo operaciones algebraicas que emplean números muy pequeños y muy grandes al mismo tiempo. Ya que este caso se presenta en muchos métodos numéricos, el error de redondeo puede resultar de mucha importancia.
Reglas de Redondeo
Las siguientes reglas dan la pauta a seguir en el redondeo de números cuando se realizan cálculos a mano.
En el redondeo, se conservan las cifras significativas y el resto se descarta. El último dígito que se conserva se aumenta en uno si el primer dígito descartado es mayor de 5. De otra manera se deja igual. Si el primer digito descartado es 5 o es 5 segundo de ceros. entonces el último dígito retenido se incrementa en 1, sólo si es impar.
En la suma y en la resta, el redondeo se lleva acabo de forma tal que el último dígito en la columna de las milésimas.
Para la multiplicación y para la división el redondeo es tal que la cantidad de cifras significativas del resultado es igual al número más pequeño de cifras significativas que contiene la cantidad en la operación.
Para combinaciones de las operaciones aritméticas, existen dos casos generales. Se puede sumar o restar el resultado o de las divisiones.
(Multiplicación o División) +/- (multiplicación o división)
o también se pueden multiplicar o dividir los resultados de las sumas y las restas.
Ejemplos
Los siguientes ejemplos tiene por objeto ilustrar las reglas de redondeo.
5.6723 -------------------------- 5.67´ 3 Cifras Significativas
10.406 ---------------------------- 7.4 4 Cifras Significativas
10.406 ---------------------------- 7.4 2 Cifras Significativas
88.21650 ------------------- 88.216 5 Cifras Significativas
1.25001 -------------------------- 1.3 2 Cifras Significativas
Errores de Truncamiento
Los errores de truncamiento son aquellos que resultan al usar una aproximación en lugar de un procedimiento matemático exacto. Además para obtener conocimineto de las características de estos errores se regresa a la formulación matemática usada ampliamente en los métodos numéricos para expresar Funciones en forma polinomial: Serie de Taylor
Por ejemplo:
La serie de Taylor provee un medio para predecir el valor de una función en un punto en términos del valor de la función y sus derivadas en otro punto.
Teorema de Taylor: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:
La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden.
Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.
El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos.
¿Cuántos términos se requieren para obtener una “aproximación razonable”?
La ecuación para el término residual se puede expresar como:
Significa que el error de truncamiento es de orden hn+1. El error es proporcional al tamaño del paso helevado a la (n+1)-ésima potencia.
Otros Tipos de Errores
Otros tipos de errores son el error humano que pueden ocurrir cuando se toman datos estadísticos o muestras, si estos datos son mal recopilados los errores al utilizarlos serán obvios. Cuando se calibran mal los equipos donde de harán lecturas de algunas propiedades de los compuestos o resultados de un experimentos. Cuando se desarrollan modelos matemáticos y estos son mal formulados y no describen correctamente el fenómeno o equipo en estudio. Todos los tipos de errores pueden contribuir a un error mayor, sin embargo el error numérico total, es la suma de los errores de truncamiento y redondeo.
Bien sea cuando realizamos una medida directa (la que da el aparato) o indirecta (utilizando una fórmula) existe un tratamiento de los errores de medida. Podemos distinguir fundamentalmente dos tipos de errores que se utilizan en los cálculos:
Error absoluto. Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
Error relativo. Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. No tiene unidades.
Además de los conceptos anteriormente señalados, podemos encontrarnos ante otros tipos de errores cuando de mediciones se trata:
Error porcentual (E%). Es el error relativo multiplicado por cien (100). Está dado por la siguiente fórmula:
E% = Er (100)
El error porcentual expresa que por cada 100 unidades medidas se comete Er de error.
Error de redondeo. Se presente cuando cortamos el número a partir de cierta cifra, pero sumamos uno a la última cifra que aparezca, en el caso de que la primera que omitamos sea mayor o igual que 5. Por ejemplo, redondeando el número π = 3.141592… a las centésimas tenemos π = 3.14, a las milésimas π = 3.142 y a las diezmilésimas π = 3.1416. En general, es preferible el redondeo al truncamiento, ya que cometemos un error menor.
Los errores de truncamiento tienen relación con el método de aproximación que se usará, ya que generalmente frente a una serie infinita de términos, se tenderá a cortar el número de términos, introduciendo en ese momento un error, por no utilizar la serie completa (que se supone es exacta).
http://matikai.com/scheme/textos/MNbS/mnbs023.pdf
http://es.wikipedia.org/wiki/Redondeo
Métodos numéricos para ingenieros 6° Ed. S.C. Chapra, R.P. Canale Ed. Mc Graw Hill
Comentarios
Publicar un comentario