Ir al contenido principal

3.4 Método de descomposición LU

 3.4 Método de descomposición LU

La factorización LU

Resultado de imagen para descomposición lu 

Supongamos que A se puede factorizar como el producto de una matriz triangular inferior L con una matriz triangular superior U:
 
A = LU (51)

En este caso, el sistema de ecuaciones dado por (44) podría representarse en la forma:
 
LUx=b (52)

Si denominamos z a la matriz columna de n filas resultado del producto de las matrices Ux, tenemos que la ecuación (52) se puede reescribir del siguiente modo:
 
Lz=b (53)

A partir de las ecuaciones (52) y (53), es posible plantear un algoritmo para resolver el sistema de ecuaciones empleando dos etapas:
  • Primero obtenemos z aplicando el algoritmo de sustitución progresiva en la ecuación (53).
  • Posteriormente obtenemos los valores de x aplicando el algoritmo de sustitución regresiva a la ecuación
    Ux = z

El análisis anterior nos muestra lo fácil que es resolver estos dos sistemas de ecuaciones triangulares y lo útil que resultaría disponer de un método que nos permitiera llevar a cabo la factorización A=LU. Si disponemos de una matriz A de $n \times n$, estamos interesados en encontrar aquellas matrices:
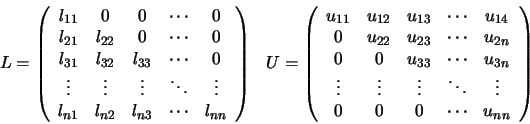
\begin{displaymath}\begin{array}{ll} L = \left( \begin{array}{ccccc} l_{11} &... ... 0 & 0 & 0 & \cdots & u_{nn} \end{array} \right) \end{array}\end{displaymath}

tales que cumplan la ecuación (51). Cuando esto es posible, decimos que A tiene una descomposición LU. Se puede ver que las ecuación anterior no determina de forma única a Ly a U. De hecho, para cada i podemos asignar un valor distinto de cero a lii o uii (aunque no ambos). Por ejemplo, una elección simple es fijar lii=1 para $i=1,2,\dots,n$ haciendo de esto modo que L sea una matriz triangular inferior unitaria. Otra elección es hacer U una matriz triangular superior unitaria (tomando uii=1 para cada i). Para deducir un algoritmo que nos permita la factorización LU de Apartiremos de la fórmula para la multiplicación de matrices:
 \begin{displaymath}a_{ij} = \sum_{s=1}^{n} l_{is}u_{sj} = \sum_{s=1}^{\mbox{\scriptsize {mín}}(i,j)} l_{is}u_{sj} \end{displaymath} (54)

en donde nos hemos valido del hecho de que lis=0 para s >i y usj=0 para s>j. En este proceso, cada paso determina una nueva fila de U y una nueva columna de L. En el paso k, podemos suponer que ya se calcularon las filas $1, 2, \dots, k-1$ de U, al igual que las columnas $1, 2, \dots, k-1$ de L. Haciendo i=j=k en la ecuación (54) obtenemos
 \begin{displaymath}a_{kk} = l_{kk}u_{kk} \sum_{s=1}^{k-1}l_{ks}u_{sk} \end{displaymath} (55)

Si especificamos un valor para lkk (o para ukk), a partir de la ecuación (55) es posible determinar un valor para el otro término. Conocidas ukk y lkk y a partir de la ecuación (54) podemos escribir las expresiones para la k-ésima fila (i=k) y para la k-ésima columna (j=k), respectivamente:
 
$\displaystyle a_{kj} = l_{kk}u_{kj} + \sum_{s=1}^{k-1} l_{ks}u_{sj}$ $\displaystyle (k+1 \leq j \leq n)$ (56)
$\displaystyle a_{ik} = l_{ik}u_{kk} + \sum_{s=1}^{k-1} l_{is}u_{sk}$ $\displaystyle (k+1 \leq i \leq n)$ (57)

Es decir, las ecuaciones (57) se pueden emplear para encontrar los elementos ukj y lik. El algoritmo basado en el análisis anterior se denomina factorización de Doolittle cuando se toman los términos lii = 1 para $1 \leq i \leq n$ (L triangular inferior unitaria) y factorización de Crout cuando se toman los términos uii=1 (U triangular superior unitaria).
Una implementación en pseudocódigo del algoritmo para llevar a cabo la factorización LU se muestra en la figura (11).


  
Figure: Implementación del algoritmo de la factorización LU.
\begin{figure} \begin{center} \begin{tabular}{\vert l\vert} \hline \\ ~~~~~... ...$u_{ij}$ ) \\ ~ \\ \hline \end{tabular} \end{center} \protect\end{figure}

Es interesante notar que los bucles que permiten el cómputo de la k-ésima fila de U y de la k-ésima columna de L se pueden llevar a cabo en paralelo, es decir, pueden evaluarse simultáneamente sobre dos procesadores, lo que redunda en un importante ahorro del tiempo de cálculo.
Ejemplo: Encuentre las factorizaciones de Doolittle y Crout de la matriz:
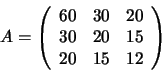
\begin{displaymath}A = \left( \begin{array}{rrr} 60 & 30 & 20 \\ 30 & 20 & 15 \\ 20 & 15 & 12 \end{array}\right) \end{displaymath}

La factorización de Doolittle es, a partir del algoritmo:
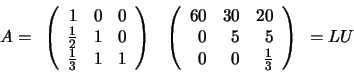
\begin{displaymath}A = \begin{array}{ll} \left( \begin{array}{rrr} 1 & 0 & 0 ... ... \\ 0 & 0 & \frac{1}{3} \end{array} \right) \end{array}= LU \end{displaymath}

En vez de calcular la factorización de Crout directamente, la podemos obtener a partir de la factorización de Doolittle que acabamos de ver. Efectivamente, si tenemos en cuenta que la matriz A es simétrica, es posible comprobar que se cumple la relación:
A = LU = UTLT

por lo que la factorización de Crout resulta ser:
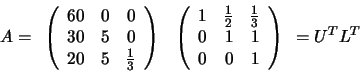
\begin{displaymath}A = \begin{array}{ll} \left( \begin{array}{rrr} 60 & 0 & 0... ... 1 \\ 0 & 0 & 1 \end{array} \right) \end{array}= U^{T}L^{T} \end{displaymath}

CODIGO MATHLAB:
function [l,u]=LUdoolitle(a)
 
n=length(a);
l=a*0; u=a*0;
for k=1:n
    u(k,k:n)=a(k,k:n)-l(k,1:k-1)*u(1:k-1,k:n);
    l(k,k)=1;
    l(k+1:n,k)=(a(k+1:n,k)-l(k+1:n,1:k-1)*u(1:k-1,k))/u(k,k);
end


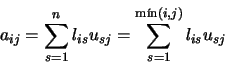
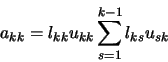
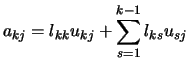
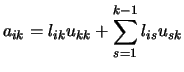
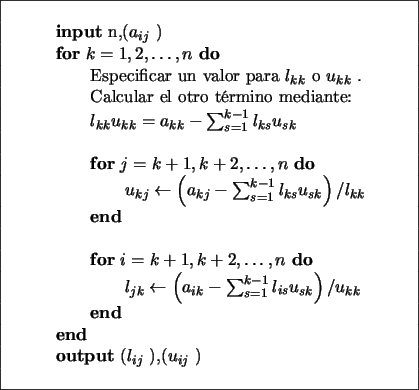
Comentarios

Publicar un comentario

Entradas populares de este blog

6.3 Métodos de pasos múltiples

6.3 Métodos de pasos múltiples Los métodos de un paso descritos en las secciones anteriores utilizan información en un solo punto xi para predecir un valor de la variable dependiente yi+1 en un punto futuro xi+1. Procedimientos alternativos, llamados métodos multipaso, se basan en el conocimiento de que una vez empezado el cálculo, se tiene información valiosa de los puntos anteriores y esta a nuestra disposición. La curvatura de las líneas que conectan esos valores previos proporciona información con respecto a la trayectoria de la solución. Los métodos multipaso que exploraremos aprovechan esta información para resolver las EDO. Antes de describir las versiones de orden superior, presentaremos un método simple de segundo orden que sirve para demostrar las características generales de los procedimientos multipaso. Observe la ecuación ec. 2  alcanza ) a expensas de emplear un tamaño de paso mas grande, 2h. Además...
Publicar un comentario
Leer más

6.2 Métodos de un paso: Método de Euler, Método de Euler mejorado y Método de Runge-Kutta

6.2 Métodos de un paso: Método de Euler, Método de Euler mejorado y Método de Runge-Kutta   Método de Euler El método de Euler es un procedimiento de integración numérica para resolver ecuaciones diferenciales ordinarias a partir de un valor inicial dado. El método de Euler es el más simple de los métodos numéricos para resolver un problema del siguiente tipo: Consiste en multiplicar los intervalos que van de x0 a xf en n subintervalos de ancho h; Osea: de manera que se obtiene un conjunto discreto de n+1 puntos: x0, x1, x2, ... , xn del intervalo de interés [x0,xf]. Para cualquiera de estos puntos de cumple que:  0<i<n. La condición inicial y(x0)=y0, representa el punto P0=(x0,y0) por donde pasa la curva solución de la ecuación del plantamiento inicial, la cual se denotará cmo F(x)=y. Ya teniendo el punto P0 se puede evaluar la primera derivada de F(x) en ese punto; por lo tanto: Con esta información se traza una recta, aquella que ...
Publicar un comentario
Leer más

2.1 Métodos de intervalos: Gráficos, Bisección y falsa posición

2.1 Métodos de intervalos: Gráficos, Bisección y falsa posición. El problema de obtener las soluciones o raíces de una ecuación algebraica o trascendente de la forma F(x)=0 se representa frecuentemente dentro el campo de la ingenierá. Se puede definir a la raíz de una ecuación como el valor de x que hace a f(x) = 0. Asi, que un método simple para obtener a la raíz de la ecuación f(x)=0, consiste en graficar la función y observar donde cruza el eje x. Por eso estos tipos de métodos, son llamados "Métodos Graficos" Debido a ello, el desarrollo de métodos que nos permiten solucionarlo es amplio; en esta unidad presentamos algunos para determinar las raíces reales o complejas de ecuaciones de este tipo, tales como: Método de Bisección o Bolzano El método de la bisección o también llamado Método de Bolzano, parte de una funcion F(x) y un intervalo [x1,x2] tal que F(x1) y F(x2) tienen signos contrarios. Si la función es continua en este intervalo, entonces existe una raíz de F(x)...
Publicar un comentario
Leer más