2.1 Métodos de intervalos: Gráficos, Bisección y falsa posición

2.1 Métodos de intervalos: Gráficos, Bisección y falsa posición.






El problema de obtener las soluciones o raíces de una ecuación algebraica o trascendente de la forma F(x)=0 se representa frecuentemente dentro el campo de la ingenierá.
Se puede definir a la raíz de una ecuación como el valor de x que hace a f(x) = 0.

Asi, que un método simple para obtener a la raíz de la ecuación f(x)=0, consiste en graficar la función y observar donde cruza el eje x. Por eso estos tipos de métodos, son llamados "Métodos Graficos"

Debido a ello, el desarrollo de métodos que nos permiten solucionarlo es amplio; en esta unidad presentamos algunos para determinar las raíces reales o complejas de ecuaciones de este tipo, tales como:

Método de Bisección o Bolzano

El método de la bisección o también llamado Método de Bolzano, parte de una funcion F(x) y un intervalo [x1,x2] tal que F(x1) y F(x2) tienen signos contrarios. Si la función es continua en este intervalo, entonces existe una raíz de F(x) entre x1 y x2.
Una vez determinado el intervalo [x1,x2] y asegura lacontinuidad de la función en dicho intervalo, se valúa ésta en el punto madion xm del intervalo:






Si F(xm) y F(x1) tiene signos contrarios, se reducirá el intervalo de x1 a xm, ya que dentro de estos valores se encuentra la raíz buscada. Al repetir este proceso, hasta lograr que la diferencia entre los dos últimos valores de xm sea menor que una tolerancia prefijada, el último valor xm será una buena aproximación de la raíz.

Pasos:
Elija valores iniciales inferior x1, y superior de x2, que encierren a la raíz, de forma que la función cambien el signo en el intervalo. Esto se verifica comprobando que f(x1) f(x2)<0
Una aproximación de la raíz, se determina mediante: Xr= x1 + x2 / 2
Realice las siguiente evaluaciones para determinar en que subintervlo ésta la raíz:
Si f(x1) f(Xr)<0, entonces la raíz se encuentra dentro del subintervalo inferior o izquierdo. Por tanto, haga X2 = Xr y vuelva al paso 2.
Si f(x1) f(Xr)>0, entonces la raíz se encuentra dentro del subintervalo superior o derecho. Por tanto, haga X1 = Xr y vuelva al paso 2.
Si f(x1) f(Xr) =0, entonces la raíz se igual a Xr; y termina el cálculo. 

Método de la Falsa Posición

Aun cuando la bisección es una técnica perfectamente válida para determinar raíces, su método de aproximación por "fuerza bruta" es relativamente ineficiente. La falsa posición es una alternativa basada en una visualización gráfica.
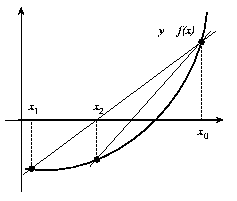
Un inconveneiente del método de bisección es que al dividir el intervalo de x1 a xu en mitades iguales, no se toman en cuenta las magnitudes de f(x1) y f(xu). Por ejemplo, si f(x1) está mucho más cercana a cero quef(xu), es lógico que la raíz se encuentre más cerca de x1 que de xu. Un método alternaticvo que aprovecha esta visualización gráfica consiste en unir f(x1) y f(xu) con una línea recta. La intersección de esta línea con el eje de las x representa un mejor aproximación de la raíz. El hecho de que se reemplace la curva por una línea recta de una "falsa posición" de la raíz; de aquí el nombre de método de la falsa posición, o en latín,regula falsi. También se le conoce como método de interpolación lineal.



Usando triángulos semejantes, la intersección de la línea recta con el eje de las x se estima mediante:



Multiplicando en cruz la ecuación anterior obtenemos:



Agrupando términos y reordenando:



Dividiendo entre



Esta es una de las formas del método de la falsa posición. Esta puede ponerse en una forma alternativa al separa los términos:



sumando y restando xu en el lado derecho:



Agrupando términos se obtiene:




o:



Esta es la fórmula de la falsa posición. El valor de xr calculado con la ecuación reemplazará, después, a cualquiera de los dos valores iniciales, xl o xu, y da un valor de la función con el mismo signo de f(xr). De esta manera, los valores xl y xu siempre encierran la verdadera raíz. El proceso se repite hasta que la aproximación a la raíz sea adecuada.

Bisección

Datos de Entrada  Intervalo con raíz Error absoluto (tolerancia de error) Numero de iteraciones (Calculado a partir del error absoluto) Este método parte de un intervalo donde debe haber un cambio de signo en los extremos al evaluar la función. Este cambio implica que la función corta el eje x y por ende en dicho intervalo existe una raíz de la función (siempre y cuando esta sea continua). Se debe aclarar que este método es el más lento pero tiene la particularidad que siempre es convergente.  El algoritmo empieza dividiendo el intervalo a la mitad, esto genera dos sub-intervalos, el algoritmo debe evaluar nuevamente en cuál de los dos subintervalos se cumple el cambio de signo al evaluar la función. De esta forma es posible desechar uno de los dos subintervalos, al subintervalo restante se le aplica el mismo procedimiento.  Al realizar este proceso varias veces se obtendrá cada vez un intervalo más ajustado. El proceso finaliza cuando el tamaño del intervalo resultante es tal que el error absolutodefinido por el usuario es mayor o igual a este. Por lo tanto la raíz puede aproximarse como el punto medio de este ultimo intervalo.    Pseudocodigo Biseccón Datos de entrada: a, b, función, error absoluto máximo Datos de Salida: Raíz, numero iteraciones Lea: f,  a, b, tol, n= redondeararriba(log((b-a)/tol)/log(2)) Si  f(a)= 0 Muestre ‘a es raíz’ Sino si f(b)= 0 Muestre ‘b es raíz’ Si no  si f(a)*f(b)<0 x=(a+b)/2 fx=f(x) i=1 error=tol+1 mientras i<=n y fx~=0 y error>tol haga si f(a)*f(x)<0 b=x sino a=x fin si aux=x x=(a+b)/2 error=abs(x-aux) fx=f(x) i=i+1 fin mientras si f(x)=0 muestre ‘La raíz es x’ sino si error<tol Muestre ‘x es una aproximación a la raíz con un error máximo de tol’ sino Muestre ‘Fracaso en n iteraciones.’ Fin si Fin si  Codigo Matlab/Octave Se debe crear un archivo .m llamado biseccion y copiar y pegar el siguiente codigo function biseccion     f=input('Ingrese la funcion: ','s');     f=inline(f);     a=input('Ingrese el limite inferior: ');     b=input('Ingrese el limite superior: ');     tol=input('Ingrese el error admisible: ');     n=ceil(log((b-a)/tol)/log(2));         if f(a)==0         fprintf('\n La raíz es: %1.10f \n',a)     else if f(b)==0         fprintf('\n La raíz es: %1.10f \n',b)         else if f(a)*f(b)<0                 fprintf('\n n  a         b         x             f(x)            \n')                    x=(a+b)/2;                 fx=f(x);                 i=1;                 error=tol+1;             while i<=n && fx~=0 && error>tol                               fprintf('%3.0f %10.10f %10.10f %10.10f %10.10f \n',i,a,b,x,f(x))                                if f(a)*f(x)<0                     b=x;                                        else                     a=x;                 end                 aux=x;                 x=(a+b)/2;                 error=abs(x-aux);                 fx=f(x);                 i=i+1;             end             if f(x)==0                 fprintf('\n La raíz es: %1.10f \n',x)             else if error<tol                 fprintf('\n %1.10f es una aproximacion a la raiz con un error maximo de %1.10f \n',x,tol)                                 else                 fprintf('\n Fracaso en %0.0f iteraciones.\n',n)                 end             end             else                 disp('El intervalo es inadecuado.')             end         end     end end Pseudocodigo Regla Falsa Datos de entrada: a, b, función, error absoluto máximo Datos de Salida: Raíz, numero iteraciones Lea: f,  a, b, tol, n= redondeararriba(log((b-a)/tol)/log(2)) Si  f(a)= 0 Muestre ‘a es raíz’ Sino si f(b)= 0 Muestre ‘b es raíz’ Si no  si f(a)*f(b)<0 x a-((f(a)*(b-a))/(f(b)-f(a))) fx=f(x); i=1; error=tol+1; mientras i<=n y fx~=0 y error>tol haga si f(a)*f(x)<0 b=x sino a=x fin si aux=x x=(a+b)/2 error=abs(x-aux) fx=f(x) i=i+1 fin mientras si f(x)=0 muestre ‘La raíz es x’ sino si error<tol Muestre ‘x es una aproximación a la raíz con un error máximo de tol’ sino Muestre ‘Fracaso en n iteraciones.’ Fin si Fin si Fin si Codigo Matlab/octave Se debe crear un archivo .m llamado reglafalsa y copiar y pegar el siguiente codigo function reglafalsa f=input('Ingrese la funcion: ','s');     f=inline(f);     a=input('Ingrese el limite inferior: ');     b=input('Ingrese el limite superior: ');     tol=input('Ingrese el error admisible: ');     n=input('ingrese el numero de iteraciones: ');         if f(a)==0         fprintf('\n La raíz es: %1.10f \n',a)     else if f(b)==0         fprintf('\n La raíz es: %1.10f \n',b)         else if f(a)*f(b)<0                 fprintf('\n n  a         b         x             f(x)            \n')                    x=a-((f(a)*(b-a))/(f(b)-f(a)));                 fx=f(x);                 i=1;                 error=tol+1;             while i<=n && fx~=0 && error>tol                               fprintf('%3.0f %10.10f %10.10f %10.10f %10.10f \n',i,a,b,x,f(x))                      % la instrucción %10.10f significa dejar 10 espacios y colocar el número con 10 decimales                        if f(a)*f(x)<0                     b=x;                                        else                     a=x;                 end                 aux=x;                 x=a-((f(a)*(b-a))/(f(b)-f(a)));                 error=abs(x-aux);                 fx=f(x);                 i=i+1;             end             if f(x)==0                 fprintf('\n La raíz es: %1.10f \n',x)             else if error<tol                 fprintf('\n %1.10f es una aproximacion a la raiz con un error maximo de %1.10f \n',x,tol)                                 else                 fprintf('\nFracaso en %0.0f iteraciones.\n',n)                 end             end             else                 disp('El intervalo es inadecuado.')             end         end     end end